Surface Areas and Volumes ⇒⇒ Exercise 11.4

Question 1

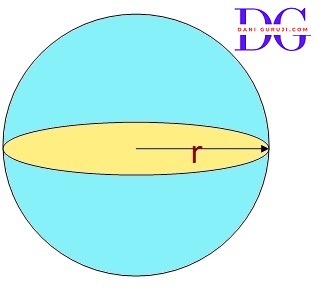
Find the volume of a sphere whose radius is
(i) 7 cm
(ii) 0.63 m (Assume π =22/7)

Solution :

Volume of a Sphere = ${ 4 \over 3}{ \pi}× r^3$

(i) Radius 7 cm

V= $ { 4 \over 3}{ \pi} r^3 $.

$$⇒ {4 \over 3} × { 22 \over 7} × 7^3 $$

$$⇒ {4 \over 3} × { 22 \over 7} × 7 × 7 × 7 $$

$$⇒ {4 \over 3} × 22 × 49 $$

$$⇒ {4312 \over 3} $$

$$⇒ 1437.33 cm^3 $$

The volume of the sphere is approximately $ {1437.33} cm^3 $

(ii) Radius 0.63 m

V= $ { 4 \over 3}{ \pi} r^3 $.

$$⇒ {4 \over 3} × { 22 \over 7} × (0.63)^3 $$

$$⇒ {4 \over 3} × { 22 \over 7} × 0.63 × 0.63 × 0.63 $$

$$⇒ {4 \over 3} × 22 × 0.09 × 0.3969 $$

$$⇒ 4 × 22 × 0.09 × 0.1323 $$

$$⇒ {1.0478} cm^3 $$

The volume of the sphere is approximately $ {1.05} cm^3 $

Question 2

Find the amount of water displaced by a solid spherical ball of diameter
(i) 28 cm
(ii) 0.21 m (Assume π =22/7)

Solution :

Volume of a Sphere = ${ 4 \over 3}{ \pi}× r^3$

Here, volume of water displaced by the given sphere = volume of the sphere

(i) Diameter = 28 cm

$$⇒ r = { 28 \over 2} $$

$$⇒ r = 14 cm $$

V= $ { 4 \over 3}{ \pi} r^3 $.

$$⇒ {4 \over 3} × { 22 \over 7} × (14)^3 $$

$$⇒ {4 \over 3} × { 22 \over 7} × 14 × 14 × 14 $$

$$⇒ {4 \over 3} × 22 × 14 × 14 × 2 $$

$$⇒ {4 \over 3} × 22 × 392 $$

$$⇒ {34,496 \over 3} $$

$$⇒ 11498.67 cm^3 $$

Thus, volume of water displaced by the given sphere ball = $ {11498.67} cm^3 $

(ii) Diameter = 0.21 m

$$⇒ r = { 0.21 \over 2} $$

$$⇒ r = 0.105 m $$

V= $ { 4 \over 3}{ \pi} r^3 $.

$$⇒ {4 \over 3} × { 22 \over 7} × (0.105)^3 $$

$$⇒ {4 \over 3} × { 22 \over 7} × 0.105 × 0.105 × 0.105 $$

$$⇒ 4 × 22 × 0.015 × 0.035 ×0.105 $$

$$⇒ 0.004851 m^3 $$

Thus, volume of water displaced by the given sphere ball = $ { 0.004851 m^3 } $

Question 3

The diameter of a metallic ball is 4.2cm. What is the mass of the ball, if the density of the metal is 8.9 g per $ cm^3 $? (Assume π =22/7)

Solution :

Volume of a Sphere = ${ 4 \over 3}{ \pi}× r^3$

Diameter = 4.2 cm

$$⇒ r = { 4.2 \over 2} $$

$$⇒ r = 2.1 cm $$

V= $ { 4 \over 3}{ \pi} r^3 $.

$$⇒ {4 \over 3} × { 22 \over 7} × (2.1)^3 $$

$$⇒ {4 \over 3} × { 22 \over 7} × 2.1 × 2.1 ×2.1 $$

$$⇒ {4 × 22 × 0.3 × 0.7 × 2.1 } $$

$$⇒ 88 × 0.441 $$

$$⇒ 38.808 cm^3 $$

The volume of the metallic ball = $ {38.808 } cm^3 $

Calculate the Mass

Mass = Volume × Density

$$ = 38.808 × 8.9 g / cm^3  $$

$$ = 345.39g  $$

Mass of the ball is 345.39 g .

Question 4

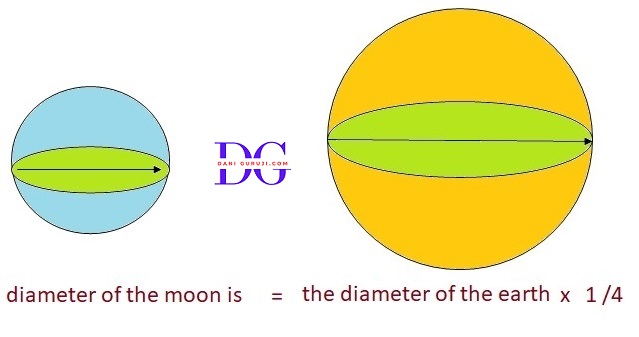
The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?(Assume π =22/7)

Solution :

Given that the diameter of the moon is approximately one-fourth of the diameter of the earth:

If diameter of earth is said d, then radius of Earth (r) = d/2

Since the diameter is twice the radius (d = 2r), this also means the radius of the moon is one-fourth of the radius of the earth .

Radius of moon = ${ 1 \over 4} × { d \over 2}$

Radius of moon = ${ d \over 8} $

Since, the earth as well as the moon are considered to be spheres.

Volume of a Sphere = ${ 4 \over 3}{ \pi}× r^3$

Find the volume of the moon

$$⇒ { 4 \over 3}{ \pi}× ({ d \over 8})^3 $$

$$⇒ {{ 4 \over 3}{ \pi}× { d^3 \over 512} }$$

Find the volume of the earth

$$⇒ { 4 \over 3}{ \pi}× ({ d \over 2})^3 $$

$$⇒ {{ 4 \over 3}{ \pi}× { d^3 \over 8}} $$

Fraction of the volume of the earth is the volume of the moon

Volume of the moon / Volume of the earth

$$⇒ { {{ 4 \over 3}{ \pi}× { d^3 \over 512} } \over {{ 4 \over 3}{ \pi}× { d^3 \over 8}} } $$

$$⇒ {{ 8 \over 512}} $$

$$⇒ {{ 1 \over 64}} $$

Volume of the moon is of the 1/64 volume of the earth.

Question 5

How many liters of milk can a hemispherical bowl of diameter 10.5cm hold? (Assume π = 22/7)

Solution :

Given, Diameter of a hemispherical bowl = 10.5 cm

Radius of hemispherical bowl = $ { 10.5 \over 2}$

= ${ 5.25 cm } $

Volume of the hemispherical bowl

Volume of a hemisphere = ${ 2 \over 3}{ \pi}× r^3 $

$$⇒ {2 \over 3}{ \pi}× (5.25)^3 $$

$$⇒ {{ 2 \over 3} × { 22 \over 7} × 5.25 × 5.25 × 5.25}$$

$$⇒ {2 × 22 × 1.75 × 0.75 × 5.25}$$

$$⇒ {44 × 6.890625}$$

$$⇒ {303.1875 cm^3}$$

Volume of the hemispherical bowl is $ {303.1875 cm^3}$

Capacity of the bowl

Now, since 1000 $ { cm^3}$ = 1 L

Therefore, 303.1875 $ { cm^3}$ of milk =$$ {{ 303.1875 \over 1000}} $$

$$⇒ {0.3031875 } L $$

Therefore, a hemispherical bowl can hold approximately 0.303 Litres of milk.

Question 6

A hemispherical tank is made up of an iron sheet 1cm thick. If the inner radius is 1 m, then find the volume of the iron used to make the tank. (Assume π = 22/7)

Solution :

The volume of the iron is the difference between the outer and inner volumes. Therefore, we need to find both the inner and outer radius.

Given Inner Radius = r = 1 m

Thickness of iron sheet = 1cm = 0.01 m

Outer Radius = The outer radius is the inner radius plus the thickness = R =

$$1 m+0.01 m=1.01 m$$

Calculate the Volume of the iron

Volume of a hemisphere = ${ 2 \over 3}{ \pi}× r^3 $

The volume of the iron is the difference between the outer hemispherical volume and the inner hemispherical volume.

The Volume of the iron $$⇒ {{2 \over 3}{ \pi}× ( R^3 - r^3 )} $$

$$⇒ {{2 \over 3}{ \pi}× ( 1.01^3 - 1^3 )}$$

$$⇒ {{2 \over 3}× { 22 \over 7} × ( 1.030301 - 1 )}$$

$$⇒ { { 44 \over 21} × ( 0.030301 )}$$

$$⇒ 0.06348 m^3$$

So, volume of the iron used in the hemispherical tank is $ 0.06348 m^3$

Question 7

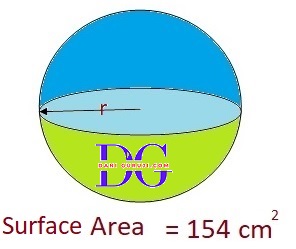
Find the volume of a sphere whose surface area is 154$cm^2$. (Assume π = 22/7)

Solution :

Surface area of sphere = 154 $cm^2$

Let the radius of the sphere be r.

Surface area = = $ 4{ \pi}× r^2$

$$ 154 = 4 × { 22 \over 7} × (r)^2 $$

$$⇒ (r)^2 = {{154 × 7} \over {22 × 4}} $$

$$ ⇒ (r)^2 ={{7 × 7} \over {4}} $$

$$ ⇒ (r)^2 =({{7 } \over {2}})^2 $$

$$ ⇒ r ={7 \over 2} = 3.5 cm. $$

The radius of the sphere is 3.5 cm

Volume of a Sphere =

$$ { 4 \over 3}{ \pi} r^3 $$

$$⇒ {4 \over 3} × { 22 \over 7} × (3.5)^3 $$

$$⇒ {4 \over 3} × { 22 \over 7} × 3.5 × 3.5 × 3.5 $$

$$⇒ {4 \over 3} × 22 × 0.5 × 3.5 × 3.5 $$

$$⇒ {4 \over 3} × 22 × 6.125 $$

$$⇒ {539 \over 3} $$

$$⇒ 179.67 cm^3 $$

Thus, volume of the given sphere = $ {179.67} cm^3 $

Question 8

A dome of a building is in the form of a hemisphere. From inside, it was white-washed at the cost of Rs. 498.96. If the cost of white-washing is at the rate of Rs. 2.00 per square meter, find:
(i) the inner surface area of the dome.
(ii) the volume of the air inside the dome.

Solution :

(i) Inside Surface Area of the Dome

The total cost of whitewashing is the inside surface area multiplied by the cost per square meter.

Inside Surface Area = The total cost / Cost per square meter.

Inside Surface Area = $ {{ 498.96} \over {2.00}} $

The inside surface area of the dome is = $ {249.48}m^2 $

(ii) Volume of the Air Inside the Dome

To find the volume of the air inside the dome (a hemisphere), you first need to find its radius

we know that, Curved surface area of a hemisphere = $ 2{ \pi}× r^2$

$$ 249.48 = 2 × { 22 \over 7} × (r)^2 $$

$$⇒ (r)^2 = {{249.48 × 7} \over {22 × 2}} $$

$$⇒ (r)^2 = {{249.48 × 7} \over {44}} $$

$$ ⇒ (r)^2 = 39.69 $$

$$ ⇒ r ={6.3} m $$

The radius of the sphere is 6.3 m

Volume of air inside the dome = Volume of hemispherical dome

Volume of a hemisphere =

$$ { 2 \over 3}{ \pi} r^3 $$

$$⇒ {2 \over 3} × { 22 \over 7} × (6.3)^3 $$

$$⇒ {2 \over 3} × { 22 \over 7} × 6.3 × 6.3 × 6.3 $$

$$⇒ {2 × 22 × 0.9 × 2.1 × 6.3} $$

$$⇒ {44 × 11.907} $$

$$⇒ 523.908 m^3 $$

The volume of the air inside the dome is approximately 523.908 $ m^3 $

Question 9

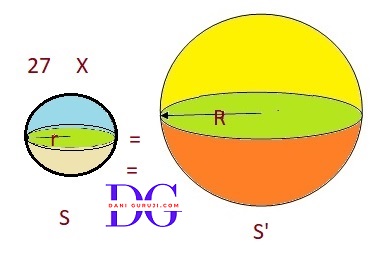
Twenty-seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S’. Find the:
(i) radius r ' of the new sphere.
(ii) ratio of S and S’.

Solution :

When 27 solid iron spheres are melted and reformed into one large sphere, the total volume of the iron remains constant.

(i) Radius of the new sphere (R)

To find the radius of the new sphere, we must equate the total volume of the 27 small spheres to the volume of the one large sphere.

Let radius of sphere be r and radius of new sphere be R.

By the principle of conservation of volume:

27 × Volume of sphere = Volume of new sphere

$$ 27 × { 4 \over 3}{ \pi} r^3 = { 4 \over 3}{ \pi} R^3 $$

$$ 27 × r^3 = R^3 $$

$$ \sqrt[3]{27 × r^3} = R $$

$$ \sqrt[3]{3^3 × r^3} = R $$

$$ 3r = R $$

The radius of the new sphere, R = 3r.

(ii) Ratio of S and S'

Surface area of one small sphere (S):

$ = 4{ \pi} r^2 $

Surface area of the new large sphere :

$S' = 4{ \pi} R^2 $

Using the new radius R =3r, we get

$ = 4{ \pi} (3r)^2 $

$ S' = 36{ \pi} r^2 $

Now, find the ratio of S to S′ :

$$⇒ {S \over S'} = { { {4{ \pi} r^2} \over {36{ \pi} r^2} } } $$

$$⇒ {S \over S'} = { { 1} \over {9} } $$

The ratio of the surface areas = 1 : 9

Question 10

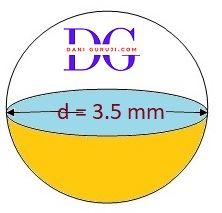
A capsule of medicine is in the shape of a sphere of diameter 3.5mm. How much medicine (in mm3) is needed to fill this capsule? (Assume π = 22/7)

Solution :

Volume of a Spherical capsule :

Diameter of capsule = 3.5 mm

Radius of capsule, say r = diameter/ 2 = 3.5 / 2 = 1.75 mm

Volume of spherical capsule

$$ { 4 \over 3}{ \pi} r^3 $$

$$ { 4 \over 3}{ \pi} ( 1.75 )^3 $$

$$ { 4 \over 3} × { 22 \over 7} × 1.75 × 1.75 × 1.75$$

$$ { 4 \over 3} × 22 × 0.25 × 1.75 × 1.75$$

$$ { 4 \over 3} × 22 × 0.7656 $$

$$ { 67.375 \over 3} $$

$$ { 22.458 }mm^3 $$

Therefore, medicine needed to fill the given capsule = 22.458 $mm^3 $